Answer:
The height of the neighboring building is 827.26 ft.
Explanation:
See the diagram attached.
Now, AB = 1100 ft and CE = h (say) and AC = b (say).
Now, from the right triangle Δ BDE,
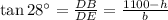 .............. (1)
.............. (1)
Again, from the right triangle Δ ABC,
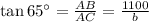
⇒ b = 512.94 ft.
Now, from equation (1) we can say

⇒ h = 827.26 ft.
Therefore, the height of the neighboring building is 827.26 ft. (Answer)