Answer:
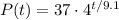
Step-by-step explanation:
This is an exponential growing: there is a constant growing factor which multiplies the value number of letters sent every week.
The growing factor 4 letters every 9.1 weeks means that every 9.1 weeks the number of letters is multiplied by 4.
Then, if the number of weeks is t, the number of times the number of letters increase is t/9.1.
Then, the exponential function that models the number of people who receive the email t weeks since Tobias initially sent the chain letter, has the form:
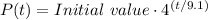
Tobias initially sent the chain letter to 37 friends; thus, the initial value is 37, and the complete function is:
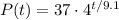 , where t is the number of weeks since Tobias initially sent the chain letter.
, where t is the number of weeks since Tobias initially sent the chain letter.