Question

A buffer that contains 0.17 M of a base, B and 0.39 M of its conjugate acid BH+, has a pH of 9.31. What is the pH after 0.02 mol of Ba(OH)2 are added to 0.72 L of the solution?

Answer 1

Answer: The pH after 0.02 mol of
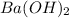`Ba(OH)_(2)` are added to 0.72 L of the solution is 9.5.

Step-by-step explanation:

The chemical equation for the dissociation of base represented by B in water is depicted as follows.

`B(aq) + H_(2)O(l) \rightleftharpoons BH^(+)(aq) + OH^(-)(aq)`

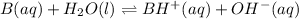
According to Henderson-Hasselbach equation,

pH =
`pK_(a) + log ([B])/([BH^(+)])`

9.31 =
`pK_(a) + log (0.17)/(0.39)`

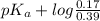
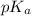`pK_(a)` = 9.31 + 0.361

= 9.671

Initial moles of B is as follows.

`0.72 L * (0.17 M)/(L)`

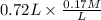
= 0.1224 mol B

Now, the initial concentration of
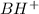`BH^(+)` is as follows.

`0.72 L * (0.39 mol)/(L)`

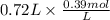
= 0.281 mol
`BH^(+)`

We will calculate the equilibrium moles after the addition of 0.02 moles
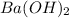`Ba(OH)_(2)` which is 0.04 moles
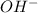`OH^(-)` as follows.

`BH^(+)(aq) + OH^(-)(aq) \rightleftharpoons B(aq) + H_(2)O(aq)`

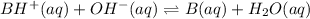
Initial: 0.281 0.04 0.1224

Change: -0.04 -0.04 +0.04

Equilbm: 0.241 0 0.1624

Hence,

pH =
`pK_(a) + log ([B])/([BH^(+)])`

=
`9.671 + log (0.1624/0.72)/(0.241/0.72)`

=
`9.671 + log (0.225/0.334)`

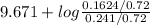
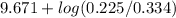
= 9.671 - 0.171

= 9.5

Thus, we can conclude that the pH after 0.02 mol of
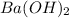`Ba(OH)_(2)` are added to 0.72 L of the solution is 9.5.