Question

A capillary tube is being used to measure the viscosity of a Newtonian liquid. The tube has a 4-cm diameter and a length of 20 cm. Estimate the viscosity coefficient for the liquid if a pressure of 2.5 kPa is required to maintain a flow 3 rate of 1 kg/s. The liquid density is 998 kg/m .

Answer 1

η = 0.783 deca poise

Step-by-step explanation:

diameter of tube, D = 4 cm

radius of tube , r = 2 cm = 0.02 m

length of the tube, l = 20 cm = 0.2 m

Pressure, P = 2.5 kPa = 2.5 x 1000 Pa

Rate of flow of mass = 1 kg/s

density of liquid, d = 998 kg/m³

Rate of flow of volume, V = mass pr unit time / density

V = 1 / 998 = 1.002 x 10^-3 m³/s

By use of Poiseulli's formula

`V = (\pi P r^(4))/(8\eta l)`

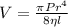
where, V is the rate of flow, P is the pressure difference between the ends of the tube, r is the radius of tube, l is the length of the tube and η is the coefficient of viscosity.

By substituting the values

`1.002* 10^(-3) = (3.14* 2.5* 10^(3)* (0.02)^(4))/(8* \eta * 0.2)`

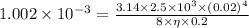
η = 0.783 deca poise