Question

A dynamics cart with a friction pad is placed at the top of an inclined track and released from rest. The cart accelerates down the incline at the rate of 0.60 m/s^2.

If the track is angled at 10 degrees above the horizontal, determine the coefficient of kinetic friction between the cart and the track.

Answer 1

The kinetic friction between the cart and the track is 0.11

Step-by-step explanation:

The force at equilibrium is equal to:

F = F´ - Fk

F = m*a

F´ = m*g*sinθ₁

Fk = uk*m*g*cosθ₁

Replacing:

m*a = m*g*sinθ₁ - uk*m*g*cosθ₁

a = g(sinθ₁ - uk*cosθ₁)

Where a = 0.6 m/s²

g = 9.8 m/s²

θ₁ = 10°

Replacing values:

0.6 = 9.8(sin(10) - uk*cos(10))

Clearing uk:

uk = 0.11

Answer 2

The coefficient of kinetic friction between the cart and the track is 0.114

Step-by-step explanation:

Given;

Angle of inclination, θ = 10°

Acceleration of the cart, a = 0.60 m/s²

Apply Newton's law of motion

mgsinθ - μkmgcosθ = ma

Divide through by mass, m

gsinθ - μkgcosθ = a

μkgcosθ = gsinθ - a

`\mu _k = (gsin \theta -a)/(gcos \theta)`

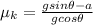
where;

μk is the coefficient of kinetic friction between the cart and the track

Substitute the given values and calculate coefficient of kinetic friction μk

`\mu _k = (gsin \theta -a)/(gcos \theta) \\\\\mu _k = (9.8sin 10 -0.6)/(9.8cos 10)\\\\\mu _k = 0.114`

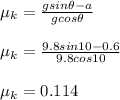
Therefore, the coefficient of kinetic friction between the cart and the track is 0.114