Question

A fisherman spots a fish underneath the water. It appears that the fish is d0 = 0.33 m under the water surface at an angle of θa = 56 degrees with respect to the normal to the surface of the water. The index of refraction of water is nw = 1.3 and the index of refraction of air is na = 1.

Answer 1

A.)
`L=d_(0) tan(\theta{a})`

B.)

Because of part A., we just plug in our given
`d{0}` and
`tan(\theta{a})`

L= .33* tan(56)

L= 0.4892451196 m

C.)
`sin(\theta{w})=(n{a}/n{w})sin(\theta{a})`

D.)

Because we are trying to isolate
`\theta{w}` from part C., we need to take the inverse sine of the right side of the equation

`sin(\theta{w})=(n{a}/n{w})sin(\theta{a})`

`\theta{w}=arcsin(n{a}/n{w})sin(\theta{a})`

now we just plug in our knowns

`\theta{w}` = arcsin( (1/1.3) sin(56)

`\theta{w}` = 41.688 degrees

E.)
`d=L/tan(\theta{w})`

F.)

Because of part E., we just need to plug in our known variables from part B. and from part D.

d = 0.4892451196/ tan(41.688)

d= 0.5493475 m

Answer 2

angle of refraction = 39.6°

Apparent depth = 0.253 m

Step-by-step explanation:

distance of fish appeared by the man inside water, Real depth , do = 0.33 m

Angle, θa = 56°

refractive index of air , na = 1

refractive index of water, nw = 1.3

Let the angle of refraction is r and the apparent depth of the fish is d.

According to the Snell's law

`n_(a)Sin\theta _(a) = n_(w)Sinr`

1 x Sin 56° = 1.3 x Sin r

Sin r = 0.6377

r = 39.6°

According to the formula of normal shift

`^(a)n_(w)=(Real depth)/(Apparent depth)`

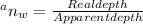
Apparent depth = 0.33/1.3

d = 0.253 m