Answer:
Therefore the rate change of the diagonal of the foam box is
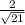 cm per minute.
cm per minute.
Explanation:
Let the length, width and height of the foam be l, w and h respectively.
The diagonal of the rectangle is d=
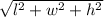
Given that, A foam box's length and width are increasing by 4 and 3 cm per minute.
Its height is decreasing by 2 cm per minute.
That is
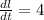 cm per min.,
cm per min.,
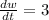 cm per min and
cm per min and
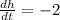 cm per min[ since the height is decreasing]
cm per min[ since the height is decreasing]
∴d=
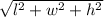
Differentiating with respect to t


Putting
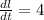 ,
,
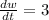 ,
,
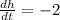
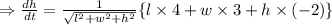
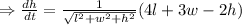
Now
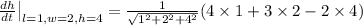
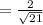
Therefore the rate change of the diagonal of the foam box is
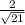 cm per minute.
cm per minute.