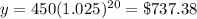Answer:
Explanation:
we know that
The equation of a exponential growth function is given by
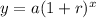
where
y is the value of the doll
x is the number of years
a is the initial value
r is the rate of change
we have
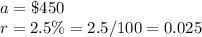
substitute
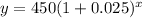
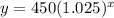
What will be the value of the doll in 20 years?
For x=20 years
substitute in the equation