Question

A laboratory scale is known to have a standard deviation (sigma) or 0.001 g in repeated weighings. Scale readings in repeated weighings are Normally distributed with mean equal to the true weight of the specimen. Three weighings of a specimen on this scale give 3.412, 3.416, and 3.414 g. A 99% confidence interval for this specimen is:

Answer 1

99% confidence interval for the given specimen is [3.4125 , 3.4155].

Explanation:

We are given that a laboratory scale is known to have a standard deviation (sigma) or 0.001 g in repeated weighing. Scale readings in repeated weighing are Normally distributed with mean equal to the true weight of the specimen.

Three weighing of a specimen on this scale give 3.412, 3.416, and 3.414 g.

Firstly, the pivotal quantity for 99% confidence interval for the true mean specimen is given by;

P.Q. =
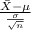`(\bar X - \mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\bar X` = sample mean weighing of specimen =
`(3.412+3.416+3.414)/(3)` = 3.414 g

`\sigma` = population standard deviation = 0.001 g

n = sample of specimen = 3

`\mu` = population mean

Here for constructing 99% confidence interval we have used z statistics because we know about population standard deviation (sigma).

So, 99% confidence interval for the population​ mean,
`\mu` is ;

P(-2.5758 < N(0,1) < 2.5758) = 0.99 {As the critical value of z at 0.5% level

of significance are -2.5758 & 2.5758}

P(-2.5758 <
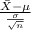`(\bar X - \mu)/((\sigma)/(√(n) ) )` < 2.5758) = 0.99

P(
`-2.5758 * {(\sigma)/(√(n) ) }` <
`{\bar X - \mu}` <
`2.5758 * {(\sigma)/(√(n) ) }` ) = 0.99

P(
`\bar X-2.5758 * {(\sigma)/(√(n) ) }` <
`\mu` <
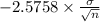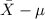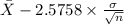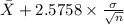`\bar X+2.5758 * {(\sigma)/(√(n) ) }` ) = 0.99

99% confidence interval for
`\mu` = [
`\bar X-2.5758 * {(\sigma)/(√(n) ) }` ,
`\bar X+2.5758 * {(\sigma)/(√(n) ) }` ]

= [
`3.414-2.5758 * {(0.001)/(√(3) ) }` ,
`3.414+2.5758 * {(0.001)/(√(3) ) }` ]

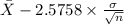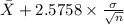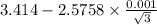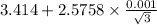= [3.4125 , 3.4155]

Therefore, 99% confidence interval for this specimen is [3.4125 , 3.4155].