Answer:
a) The speed of the slider is 4.28 in/s
b) The velocity vector is 2.33 in/s
Step-by-step explanation:
a) According to the diagram 1 in the attached image:
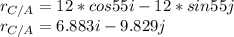
Also:
![v_(C) =v_(A)+w_(AC)*r_(C/A)\\v_(Ci)=-3j+\left[\begin{array}{ccc}i&j&k\\0&0&w_(AC) \\6.883&-9.829&0\end{array}\right]\\v_(Ci)=-3j+(0+9.829w_(AC) i-(0-6.883w_(AC))j\\v_(Ci)=9.829w_(AC)i+(-3+6.883w_(AC))j](https://img.qammunity.org/2021/formulas/physics/college/8evtfzrkdu8nopo8uv9wlvivtxufxdrkkm.png)
If we comparing both sides of the expression:
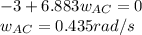
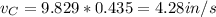
b) According to the diagram 2 in the attached image:
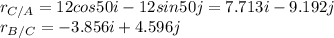
![v_(C)=v_(A)+w_(AC)r_(C/A)\\v_(C)=-3j+\left[\begin{array}{ccc}i&j&k\\0&0&w_(AC)\\7.713&-9.192&0\end{array}\right] \\v_(Ci)=-3j+(9.192w_(AC))i+7.713w_(AC)j\\v_(Ci)=9.192w_(AC)i+(7.713w_(AC)-3)j](https://img.qammunity.org/2021/formulas/physics/college/wbnh3o41b8wv5rmys3qfkd36xuejqox2d3.png)
Comparing both sides of the expression:

![v_(B)=v_(C)+w_(AC)r_(B/C)\\v_(B)=3.57i+\left[\begin{array}{ccc}i&j&k\\0&0&0.388\\-3.856&4.59&0\end{array}\right] \\v_(B)=3.57i+(0-1.78)i-(0+1.499)j\\v_(B)=1.787i-1.499j\\|v_(B)|=\sqrt{1.787^(2)+1.499^(2) } =2.33in/s](https://img.qammunity.org/2021/formulas/physics/college/9dj9zj6ft5kn3mgw5t41fjs345itae64nx.png)