Question

A hydraulic cylinder causes the distance between points A and O to decrease at a constant rate of 3 inches per second. a) Determine the speed of the slider when the support bar [OB] orientation angle, theta , is 55 degrees. b) Determine the velocity vector of the center of the bar [ABC] when , theta = 50° .

Answer 1

a) The speed of the slider is 4.28 in/s

b) The velocity vector is 2.33 in/s

Step-by-step explanation:

a) According to the diagram 1 in the attached image:

`r_(C/A) =12*cos55i-12*sin55j\\r_(C/A)=6.883i-9.829j`

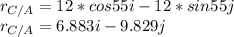
Also:

`v_(C) =v_(A)+w_(AC)*r_(C/A)\\v_(Ci)=-3j+\left[\begin{array}{ccc}i&j&k\\0&0&w_(AC) \\6.883&-9.829&0\end{array}\right]\\v_(Ci)=-3j+(0+9.829w_(AC) i-(0-6.883w_(AC))j\\v_(Ci)=9.829w_(AC)i+(-3+6.883w_(AC))j`

If we comparing both sides of the expression:

`-3+6.883w_(AC)=0\\w_(AC)=0.435rad/s`

`v_(C)=9.829*0.435=4.28in/s`

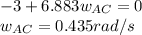
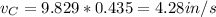
b) According to the diagram 2 in the attached image:

`r_(C/A)=12cos50i-12sin50j=7.713i-9.192j\\r_(B/C)=-3.856i+4.596j`

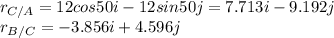
`v_(C)=v_(A)+w_(AC)r_(C/A)\\v_(C)=-3j+\left[\begin{array}{ccc}i&j&k\\0&0&w_(AC)\\7.713&-9.192&0\end{array}\right] \\v_(Ci)=-3j+(9.192w_(AC))i+7.713w_(AC)j\\v_(Ci)=9.192w_(AC)i+(7.713w_(AC)-3)j`

Comparing both sides of the expression:

`7.713w_(AC)-3=0\\w_(AC)=0.388rad/s\\v_(C)=3.575i`

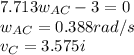
`v_(B)=v_(C)+w_(AC)r_(B/C)\\v_(B)=3.57i+\left[\begin{array}{ccc}i&j&k\\0&0&0.388\\-3.856&4.59&0\end{array}\right] \\v_(B)=3.57i+(0-1.78)i-(0+1.499)j\\v_(B)=1.787i-1.499j\\|v_(B)|=\sqrt{1.787^(2)+1.499^(2) } =2.33in/s`