Question

A new gel is being developed to use inside padding and helmets to cushion the body from impacts. The gel is stored in a 4.24.2 cubic meters [m cubed ]m3 cylindrical tank with a diameter of 2 meters​ [m]. The tank is pressurized to 1.41.4 atmosphere​ [atm] of surface pressure to prevent evaporation. A total pressure probe located at the bottom of the tank reads 6565 feet of water​ [ft Upper H 2 Upper OH2O​]. What is specific gravity of the gel contained in the​ tank?

Answer 1

The specific gravity of the gel is 1470.68

Step-by-step explanation:

Given:

Volume
`V = 4.24`
`m^(3)`

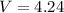
Diameter of tank
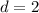`d = 2` m

Pressure at surface
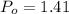`P _(o) = 1.41` atm

Height
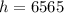`h = 6565` ft
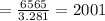`= (6565)/(3.281) = 2001` m

Pressure at bottom is given by,

`P_(bottom) = \rho _(w) g h`

Where
`\rho _(w) = 1000 (kg)/(m^(3) )`,
`g = 9.8(m)/(s^(2) )`

`P_(bottom) = 1000 * 9.8 * 2001`

`P_(bottom) = 19.6 * 10^(6)`
`(N)/(m^(2) )`

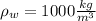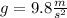
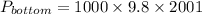
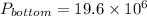
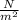
Here volume is 4.24
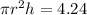
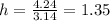`m^(3)`

`\pi r^(2) h = 4.24`

`h = (4.24)/(3.14) = 1.35` m

From pascal equation,

`P_(bottom) = P_(o) + \rho _(gel) g h`

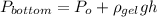
Find density of gel from above equation,

`19600000 = 142865.25 + \rho_(gel) * 9.8 * 1.35`

`\rho_(gel) = 1470682.89`
`(kg)/(m^(3) )`

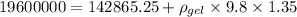
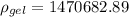
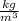
So specific gravity is given by,

ζ =
`(\rho _(gel) )/(\rho_(w) )`

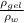
ζ =
`(1470682.89)/(1000)`

ζ =
`1470.68`

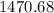
Therefore, the specific gravity of the gel is 1470.68