Question

A parallel plate capacitor filled with air with plate area 2-cm2 and plate separation of 0.5 mm is connected to a 12 V batter and fully charged. The battery is then disconnected. a) What is the charge on the capacitor? b) The plates are now pulled to a separation of 0.75 mm. What is the charge on the capacitor now? c) What is the potential difference across the plates now? d) How much work was required to pull the plates to their new separation?

Answer 1

(a) The charge on the capacitor, Q = 42.5 pC

b) The new charge on the capacitor, Q = 42.5 pC

c) New voltage across the capacitor, V = 18.0 V

d) Work done, W = 127.5 pJ

Step-by-step explanation:

The capacitance of a parallel plate capacitor is given by the relation:

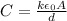`C = (k \epsilon_(0)A )/(d)`..................(1)

Area of plate,
`A = 2 cm^(2) = 2 * 10^(-4) m^(2)`

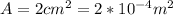
For air, dielectric constant k = 1

Initial potential difference, V₀ = 12.0 V

Separation between the plates, d = 0.50 mm = 0.50 x 10⁻³ m

The charge on the capacitor can be given by the equation

`Q = C V_(0)`...............(2)

Putting appropriate values into equation (1)

`C = (1 * 8.854 * 10^(-12)* 2 * 10^(-4) )/(0.5 * 10^(-3) )`

`C = 3.542 * 10^(-12) F`

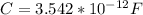
Inserting the value of C into equation (2)

`Q = 3.542 * 10^(-12) * 12\\Q = 42.5 * 10^(-12) C\\Q = 42.5 pC`

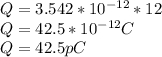
(b) Since the battery has been disconnected from the capacitor, the charge on the capacitor does not change despite the increase in the separation between the plates

`Q = 42.5 * 10^(-12) C`

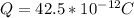
(c) New potential difference between the plates,

Since the charge remains the same after the disconnection

`Q_(f) = Q_(i)`

`C_(f) V_(f) = C_(i) V_(i)`

`(k \epsilon_(0)A )/(d_(f) )V_(f) = (k \epsilon_(0)A )/(d_(i) )V_(i)`

`(V_(f) )/(d_(f) ) = (V_(i) )/(d_(i) ) \\(V_(f) )/(0.75 * 10^(-3) ) = (12 )/(0.5 * 10^(-3) ) \\V_(f) = (12 *0.75 * 10^(-3) )/(0.5 * 10^(-3)) \\V_(f) = 18.0 V`

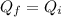
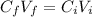
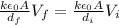
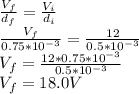
The new potential difference across the plates is 18 V

(d) Amount of Work required to pull the plates to their new separation -

`W = (1)/(2) q(V_(2) - V_(1) )\\W = (1)/(2) * 42.5 * 10^(-12) (18-12 )\\W = 0.5 * 42.5 * 6 * 10^(-12)\\W = 127.5 * 10^(-12) J\\W = 127.5 pJ`

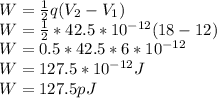
Work done = 127.5 pJ

Answer 2

a) The charge of the capacitor is 4.25x10⁻¹¹C

b) The charge of the capacitor is 4.25x10⁻¹¹C because the battery is disconnected.

c) The potential difference across the plates is 18 V

d) The work is 7.64x10⁻¹⁰J

Step-by-step explanation:

The capacitance of the capacitor is equal to:

`C=(e_(0)A )/(d)`

A = 2 cm² = 0.0002 m²

d = 0.5 mm = 0.0005 m

Replacing:

`C=(8.85x10^(-12)*0.0002 )/(0.0005) =3.54x10^(-12) F = 3.54pF`

a) The charge of the capacitor is equal to:

Q = C*V = 3.54 * 12 = 42.48 pC = 4.25x10⁻¹¹C

b) The charge is the same because the battery is disconnected (Q = 4.25x10⁻¹¹C)

c) If distance is increased, we have:

`C=(8.85x10^(-12)*0.0002 )/(0.00075) =2.36x10^(-12) F=2.36pF`

The potential is:

`V=(Q)/(C) =(42.48)/(2.36) =18V`

d) The work done is equal to:

`W=VQ=18*42.48=764.6pJ=7.64x10^(-10) J`