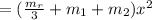Answer:
The moment of inertia of the assembly is
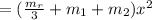
Step-by-step explanation:
Moment of inertia of a rod of mass M and length L about its center is given by

Substitute
 for M and 2x for L
for M and 2x for L

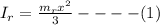
Moment of inertia of mass
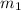 , distance x from the axis:
, distance x from the axis:
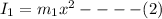
Moment of inertia of mass
 , distance x from the axis:
, distance x from the axis:
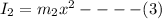
The moment of inertia of each of the components is found out. Moment of inertia of point particle with mass MM is given by the product of its mass and the square of its distance from the axis
The total moment of inertia of the system is given by:
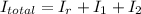
Substitute from
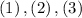 to the above relation:
to the above relation:
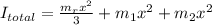
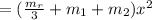
The moment of inertia of the assembly is