Question

It takes Cookie Cutter Modular Homes, Inc., about six days to receive and deposit checks from customers. Cookie Cutters management is considering a lockbox system to reduce the firm's collection times. It is expected that the lockbox system will reduce receipt and deposit times to three days total. Average daily collections are $133,000 and the required rate of return is 5 percent per year. Assume 365 days per year.

1. What is the reduction in outstanding cash balances as a result of implementing the lockbox system?

Cash balance reduction=$?

2. What is the daily dollar return that could be earned on these savings? (round your answer to 2 decimal places. (e.g 32.16))

Dollar return= $?

3. What is the maximum monthly charge cookie cutter should pay for this lockbox system if the payment is due at the end of the month? (round your answers to 2 decimal places. (e.g. 32.16))

Maximum monthly charge= $?

4. What is the maximum monthly charge cookie cutter should pay for this lockbox system if the payment is due at the beginning of the month? (round your answer to 2 decimal places (e.g.32.16))

Maximum monthly charge= $?



Please show all work and label each answer as following:

Cash balance reduction= $?

Dollar return=$?

Maximum monthly charge end of each month= $?

Maximum monthly charge beginning of the month= $?

Answer 1

a) Cash balance reduction= $399,000

b) Dollar return= $53.34

c) Maximum monthly charge end of each month = $1625.53

d) Maximum monthly charge beginning of the month = $1618.93

Step-by-step explanation:

Given:

•Average daily collections = $133,000

• Daily required rate of return = 5%

a) To find the cash balance reduction, we have:

3days * $133,000 = $399,000

b) let's use the frormula:

`(1 + r)^(^1)/(^3^6^5) - 1`

=
`(1 + 0.5)^(^1)/(^3^6^5) - 1`

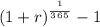
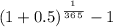
= 0.00013368

Therefore, the dollar return will be:

$399,000 * 0.00013368 = $53.33833

Dollar return = $53.34

c) we need to find the monthly rate:

`(1 + 0.5)^(^1)/(^1^2) - 1`

`= (1.05)^(^1)/(^1^2) - 1`

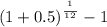
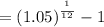
= 1.004074 - 1 = 0.004074

Max monthly charge at end of month wil be:

$399,000 * 0.004074 = $1625.526

d)
`(1 + 0.06)^(^1)/(^1^2) - 1 =`

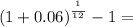
1.004074 - 1 = 0.004074

Max monthly charge at beginning of the month:

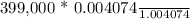`($399,000 * 0.004074)/(1.004074)` = $1618.9305