Given:
Given that the functions
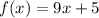 and
and
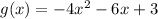
We need to determine the value of the function
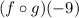
First, we shall determine the value of the function
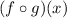
The value of the function
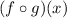 :
:
Let us determine the value of the function
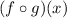
Thus, we have;
![(f \circ g)(x)=f[g(x)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/hc65fx601ckp75xr4qftkxf11k7eqtpy7p.png)
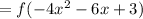
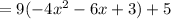
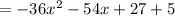
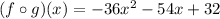
Thus, the value of the function is
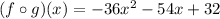
The value of the function
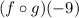 :
:
The value of the function
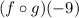 can be determined by substituting x = -9 in the function
can be determined by substituting x = -9 in the function
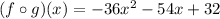
Thus, we have;
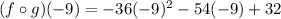
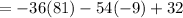
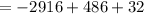
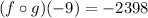
Thus, the value of the function
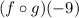 is -2398
is -2398
Hence, Option A is the correct answer.