Question

Suppose a life insurance company sells a ​$260 comma 000 ​one-year term life insurance policy to a 25​-year-old female for ​$230. The probability that the female survives the year is 0.999572. Compute and interpret the expected value of this policy to the insurance company.

Answer 1

The probability of no survive by the complement rule is
`q = 1-p = 1-0.999572=0.000428`

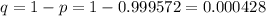
And the expected value would be given by:

`E(X) = 230*0.999572 - 0.000428*260000 = 118.621`

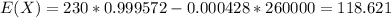
So then the company would expect a net amount of 118.621 for the insurance.

Step-by-step explanation:

Previous concepts

The expected value of a random variable X is the n-th moment about zero of a probability density function f(x) if X is continuous, or the weighted average for a discrete probability distribution, if X is discrete.

The expected value is defined by this formula:

`E(X) = \sum_(i=1)^n X_i P(X_i)`

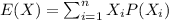
Where
`X_i , i =1,2,...,n` represent the possible values for the random variable and
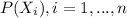`P(X_i) , i =1,...,n` the corresponding probabilities.

Solution to the problem

For this case we define X a random variable who represent the net amount of money for the company.

The probability of no survive by the complement rule is
`q = 1-p = 1-0.999572=0.000428`

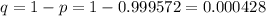
And the expected value would be given by:

`E(X) = 230*0.999572 - 0.000428*260000 = 118.621`

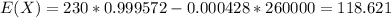
So then the company would expect a net amount of 118.621 for the insurance.