Answer:
Explanation:
You have to complete the square in order to find the center and the radius of this. Let's begin by putting it in sort-of standard form. I'm going to move thee 4 over to the other side by the 36:
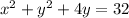
You should be able to tell right away, if you are at this point in your learning about circles, that the h coordinate of the center is 0. There is no linear term for the x, only a squared term. The linear term is the one that dictates the side to side movement. If there is no linear, or x-term, the circle does not move from x = 0. But there is a linear term on the y. It is 4y. So while we cannot complete the square on the x term, we can on the y. The rule is to take half the linear term, square it, and add that squared value in to both sides. Our linear y term is 4. Half of 4 is 2, and 2 squared is 4. So we add 4 to both sides:
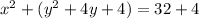
The reason you complete the square is to get to the perfect square binomial which will tell you what the center is. I will state the binomial on the left along with simplifying on the right:
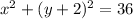
That''s the standard form of that circle. The center is (0, -2) and the radius is the square root of 36 which is 6.