Question

A three-phase wye-connected synchronous generator supplies a network through a transmission line. The network can absorb or deliver power while maintaining its terminal voltage constant. The four-pole, 60 Hz generator data rating are 40 MVA and 26 kV with a 0.85 p.u. reactance. The field current of the generator can be adjusted to regulate the excitation (induced) voltage from 0.75 to 1.5 times the rated voltage. The network voltage rating is 24 kV. The transmission line impedance and length are 0.07+j0.5 Ω/mi and 8 mi.

Calculate the generator induced voltage versus power factor, if the network voltage is at the rated value, and the bus absorbs the generator rated power. After this, plot the voltage regulation of the system versus the power factor. Use the induced voltage and network voltage for plotting the voltage regulation. The leading power factor varies from 0.5 to 1. What power factor corresponds to 10% regulation?

Answer 1

the graph and the answer can be found in the explanation section

Step-by-step explanation:

Given:

Network rated voltage = 24 kV

Impedance of network = 0.07 + j0.5 Ω/mi, 8 mi

Rn = 0.07 * 8 = 0.56 Ω

Xn = 0.5 * 8 = 4 Ω

If the alternator terminal voltage is equal to network rated voltage will have

Vt = 24 kV/√3 = 13.85 kV/phase

The alternative current is

`I_(a) =(40x10^(6) )/(√(3)*24x10^(3) ) =926.2A`

`X_(s) =0.85(13.85)/(926.2) =12.7ohm`

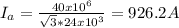
The impedance Zn is

`\sqrt{0.56^(2)+4^(2) } =4.03ohm`

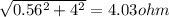
The voltage drop is

`I_(a) *Z_(n) =926.2*4.03=3732.58V`

`r_(dc) =(voltage)/(2*current) =(13.85)/(2*926.2) =7.476ohm`

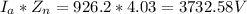
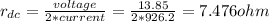
rac = 1.2rdc = 1.2 * 7.476 = 8.97 Ω

The effective armature resistance is

`Z_(s) =\sqrt{R_(a)^(2)+X_(s)^(2) } =\sqrt{8.97^(2)+12.7^(2) } =15.55ohm`

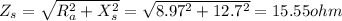
The induced voltage for leading power factor is

`E_(F) ^(2) =OB^(2) +(BC-CD)^(2)`

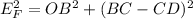
if cosθ = 0.5

`E_(F) =\sqrt{(13850*0.5)^(2)+((3741)/(2)-926.2*12.7)^(2) } =11937.51V`

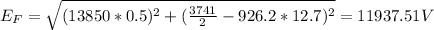
if cosθ= 0.6

EF = 12790.8 V

if cosθ = 0.7

EF = 13731.05 V

if cosθ = 0.8

EF = 14741.6 V

if cosθ = 0.9

EF = 15809.02 V

if cosθ = 1

EF = 13975.6 V

The voltage regulation is

`(E_(F)-V_(t) )/(V_(t) ) *100`

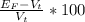
For each value:

if cosθ = 0.5

voltage regulation = -13.8%

if cosθ = 0.6

voltage regulation = -7.6%

if cosθ = 0.7

voltage regulation = -0.85%

if cosθ = 0.8

voltage regulation = 6.4%

if cosθ = 0.9

voltage regulation = 14%

if cosθ = 1

voltage regulation = 0.9%

the graph is shown in the attached image

for 10% of regulation the power factor is 0.81