Question

The lengths of corresponding sides of two squares are in the ratio of 3:1. If the area of the larger square exceeds the area of the smaller square by 63 in.², find the area of the smaller square

Answer 1

The area of the smaller square is 7.875 square inches

Explanation:

we know that

If two figures are similar, then the ratio of its areas is equal to the scale factor squared

Remember that all the squares are similar

Let

z ----> the scale factor

x ---> the area of the larger square

y ---> the area of the smaller square

so

`z^2=(x)/(y)`

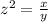
we have

`z=(3)/(1)=3` ---> scale factor

substitute

`3^2=(x)/(y)`

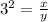
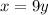`x=9y` ----> equation A

That means---> the area of the larger square is 9 times greater than the area of the smaller square

The area of the larger square exceeds the area of the smaller square by 63 in.²

so

`x=y+63` ----> equation B

Equate equation A and equation B

`9y=y+63`

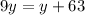
solve for y

`9y-y=63\\8y=63\\y=7.875\ in^2`

therefore

The area of the smaller square is 7.875 square inches