The question is missing some informations. Here they are:
Suppose that the times taken for germination for cauliflower seeds are normally distributed with a mean of 6.9 days. Suppose that also exactly 85% of the cauliflower seeds germinate in 6 days or more. Find the standard deviation of times taken for germination for cauliflower seeds. Carry your intermediate computations to at least four decimal places. Round your anwer to at least two decimal places.
Answer: σ = 0.98
Step-by-step explanation: Standard Deviation is the measure of how spread the numbers are, in other words, how different the numbers are in relation to the mean. That's why standard deviation is related to mean.
To calculate it, you can use:
σ = √∑(x - μ)² / n
where:
x is the individual value;
μ is the mean of the data set;
n is the quantity the sample has;
For this question, the sample is 85% of seeds, so n = 0.85.
Substituing the formula with the data given:
σ =

σ =

σ =
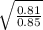
σ = 0.98
Therefore, Standard Deviation is 0.98.