Question

A triangle has vertices A(1, 1), B(2, 4), and C(4, 2). Line p is parallel to side AB and contains point C.

Write an equation for line p.

Part I: Find the slope of AB. Show your work.

Part II: Use the slope from Part I and point C to write an equation for line p in slope-intercept form.

Show your work

Answer 1

`p:y = 3x-10`

Explanation:

We are given the following in the question:

A(1, 1), B(2, 4), C(4, 2)

i) Slope of AB

`A(1, 1), B(2, 4)\\\\m = (y_2-y_1)/(x_2-x_1)\\\\m = (4-1)/(2-1)=3`

Thus, slope of AB is 3.

ii) Point slope form

The point slope form of a line can be written as:

`y - y_1 = m(x - x_1)`

The point intercept form of line can be written as:

`y = mx + c`

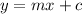
The line is parallel to AB and contains point C(4, 2). Since line p is parallel to AB, line p will have the same slope as line AB

Putting values, we get,

`y - 2 = 3(x-4)\\y = 3x-12+2\\y = 3x-10`

which is the required slope intercept equation of line p.