75 weeks takes for the amount of water in the two tanks be the same, if a 1200 gallons water tank leaking rate of 5 gallons per week and 1500 gallons water tank leaking rate of 9 gallons per week.
Explanation:
The given is ,
First water tank holds 1200 gallons and leaking at a rate of 5 gallons per week.
Second water tank holds 1500 gallons and leaking at a rate of 9 gallons per week.
Step:1
The difference in the water level in tanks,
= Second tank - First tank
= 1500 - 1200
= 300 gallons
Step:2
The difference in the rate of leaking of water in tanks,
= Rate of leaking of second tank - rate of leaking of first tank
= 9 - 5
= 4 gallons per week
Step:3
Weeks takes for the two tanks are same level of water,
=
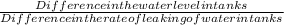
=

= 75 weeks
Step:4
Check for solution,
Water at the first tank after 75 weeks,
= Total capacity - Amount of water leaked at 75 weeks
= 1200 - ( 5 × 75)
= 825 gallons
Water at the second tank after 75 weeks,
= Total capacity - Amount of water leaked at 75 weeks
= 1500 - ( 9 × 75)
= 825 gallons
Water at the first tank after 75 weeks = Water at the second tank after 75 weeks,
825 gallons = 825 gallons
Result:
75 weeks takes for the amount of water in the two tanks be the same, if a first water tank holds 1200 gallons at a leaking rate of 5 gallons per week and second water tank holds 1500 gallons at a leaking rate of 9 gallons per week.