Question

According to observer O, a blue flash occurs at xb = 10.4 m when tb= 0.124 μs, and a red flash occurs at xr= 23.6 m when tr= 0.138 μs. According to observer O’, who is in motion relative to O at velocity u, the two flashes appear to be simultaneous. Find the velocity u.

Answer 1

u = 95.46 * 10⁶ m/s

Step-by-step explanation:

For the first observer O,

Time of the blue flash,
`t_(b) = 0.124 \mu s`

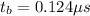
Time of the red flash,
`t_(r) = 0.138 \mu s`

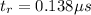
Distance covered before the blue flash,
`x_(b) = 10.4 m`

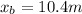
Distance covered before the red flash,
`x_(r) = 23.6 m`

Difference in time observed by the first observer O, Δt =
`t_(r) - t_(b)`

Δt = 0.138 - 0.124 = 0.014 μs

Difference in the distance observed by the observer O, Δx =
`x_(r) - x_(t)`

Δx = 23.6 m - 10.4 m

Δx = 13.2 m

Since for the observer O', the two flashes are simultaneous, there will be no time difference between the two flashes. i.e. Δt' = 0

Using the lorent'z transformation equation:

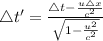`\triangle t' = \frac{\triangle t - (u \triangle x)/(c^(2) ) }{\sqrt{1 - (u^(2) )/(c^(2) ) } }`...................(1)

But Δt' = 0,

equation (1) becomes

`0 = \triangle t - (u \triangle x)/(c^(2) ) \\`

`0 = (0.014 * 10^(-6) ) - (u * 13.2)/((3*10^(8)) ^(2) )`

`(0.014 * 10^(-6) ) = (u * 13.2)/((3*10^(8)) ^(2) ) \\u = 95454545.46 m/s`

u = 95.46 * 10⁶ m/s

Answer 2

The velocity is
`u=0.3m/s`

Step-by-step explanation:

From the question we can deduce that both flashes occurred simultaneous to the observer

So the first derivative of the time difference
`\Delta t' =0`

Generally the Lorentz transformation i mathematically denoted as

`\Delta t' = \frac{ \Delta t -(v \Delta x)/(c^2) }{\sqrt{1-(v^2)/(c^2) } }`

=>
`0 = \frac{ \Delta t -(v \Delta x)/(c^2) }{\sqrt{1-(v^2)/(c^2) } }`

=>
`\Delta t -(u \Delta x )/(c^2) = 0`

Now making u the subject

`u = (c^2 \Delta t )/(\Delta x)`

`= (t_b - t_r)/(x_b - x_r) c^2`

substituting
`0.24 \mu s = 0.24*10^(-6)s` for
`t_b` ,
`0.138 \mu s = 0.138*10^(-6)s` for
`t_r` ,
`10.4 m` for
`x_b` ,
`23.6 m` for
`x_r` and
`3.0*10^8 m/s` for c

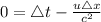
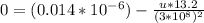
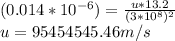
`u = \frac{0.124*10^ {-6} -0.138 *10^(-6)}{10 - 23.6}`

`u=0.3m/s`