Question

What is a5 in the sequence defined as follows?
an = 5x2^(n-1)

Answer 1

Given:

The nth term of the sequence is defined as
`a_n=5* 2^(n-1)`

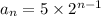
We need to determine the term
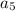`a_5` of the sequence.

The term
`a_5`:

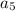The term
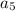`a_5` can be determined by substituting n = 5 in the nth term of the sequence
`a_n=5* 2^(n-1)`

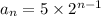
Thus, we get;

`a_5=5* 2^(5-1)`

Simplifying the expression, we get;

`a_5=5* 2^(4)`

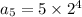
Squaring the term, we have;

`a_5=5* 16`

Multiplying the expression, we get;

`a_5=80`

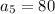
Thus, the value of the term
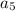`a_5` of the sequence is 80.