Answer:
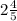 hours.
hours.
Explanation:
We have been given that a cylindrical water tank is being filled with a hose. The depth of the water increases by 1 1/4 ft per hour. We are asked to find the time taken for the water level in the tank to be 3 1/2 ft deep.
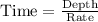
Let us convert our given mixed fractions into improper fractions as:
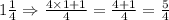
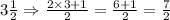
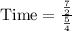
Using rule
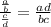 , we will get:
, we will get:
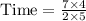
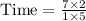
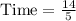
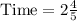
Therefore, it will take
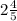 hours for the water level in the tank to be
hours for the water level in the tank to be
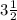 feet deep.
feet deep.