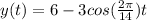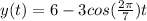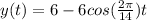Answer:
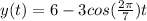
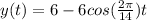

Explanation:
Given that,
Hudson Bay tides vary between
 and
and
 .
.
Tide is at its lowest when
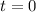
Completes a full cycle in 14 hours.
To find:- What is the amplitude, period, and midline of a function that would model this periodic phenomenon?
So, The periodic function of this model is
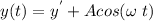 ...................(1)
...................(1)
where,

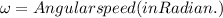
Then putting the value in given Equation(1) we get,
Amplitude =

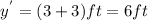
Now, At
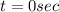 it complete full cycle in
it complete full cycle in
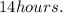
 because it is at lowest at t=0sec.
because it is at lowest at t=0sec.
∵

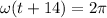
∴
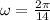
Hence