Answer:
(1)We get that all terms have same
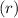 then It is a Geometric Sequence.
then It is a Geometric Sequence.
(2)We get Common ratio of given sequence is not same. It is not an geometric sequence.
(3)We get the common ratio is same then it is a Geometric Sequence
(4)We get the common ratio is same then it is a Geometric Sequence.
(5)We get Common ratio of given sequence is not same. It is not an geometric sequence.
Explanation:
Here, The Geometric Progression in the form:

Where
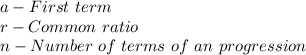
So, Check all that apply.
(1)

For the geometric Sequence Common ratio
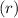 must be same.
must be same.
⇒
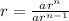
Then, Finding
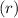 for given sequence
for given sequence
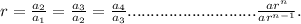
∴
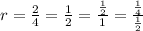
⇒
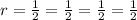
Clearly,
We get that all terms have same
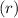 then It is a Geometric Sequence.
then It is a Geometric Sequence.
(2)
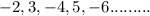
Same as above we will check the common ratio
⇒
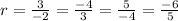
⇒
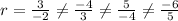
Clearly,
We get Common ratio of given sequence is not same. It is not an geometric sequence.
(3)
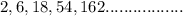
Now checking common Ratio
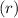
⇒
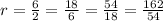
⇒
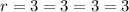
Therefore,
We get the common ratio is same then it is a Geometric Sequence.
(4)

Now checking common Ratio
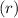
⇒
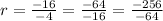
⇒
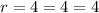
Therefore,
We get the common ratio is same then it is a Geometric Sequence.
(5)
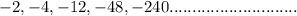
Now checking common Ratio
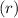
⇒
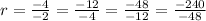
⇒
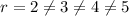
Clearly,
We get Common ratio of given sequence is not same. It is not an geometric sequence.