Question

A mass of 16 kg stretches a spring 4.9 cm. The mass moves in a medium that imparts a viscous force of 4 N when the speed of the mass is 1 cm/s. The mass is set in motion from its equilibrium position with an initial upward velocity of 5 cm/s. No external force is applied. Write the IVP so that u would be in meters if solved.

Answer 1

The initial value problem is given by

16 u'' + 400 u' + 3203 u = 0 , u (o) = 0 & u' (0) = 0.05
`(m)/(s)`

Step-by-step explanation:

Given data

m = 16 kg

L = 4.9 cm = 0.049 m

Viscous force F = 4 N

Sped of the mass u' (t) = 1
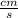`(cm)/(s)` = 0.01
`(m)/(s)`

u (o) = 0

u' (0) = 0.05
`(m)/(s)`

We know that
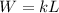
`W = k L`

K =
`(16 (9.81))/(0.049)`

k = 3203
`(N)/(m)`

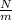
This is the stiffness of the spring.

We know that viscous force F = c u' (t)

Where c = damping constant

`c = (4)/(0.01)`

C = 400 N

Therefore the initial value problem is given by

m u'' + c u' + k u = 0

16 u'' + 400 u' + 3203 u = 0 , u (o) = 0 & u' (0) = 0.05
`(m)/(s)`