Answer:
a)

b)
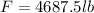
c)

Explanation:
a) The hydrostatic pressure equation is given by:
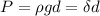
- ρ is the weight density of water (ρ = 62.5 lb/ft³)
- d is the deep of the aquarium (d = 5 ft)
So P will be:

b) The hydrostatic force of the bottom of the aquarium will be:
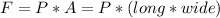

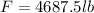
c) Here we first need to find the horizontal slice of with dx and ad deep x.
The area of this strip is: dA = 3*dx.
So the force will be:
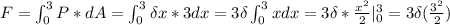
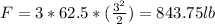
I hope it helps you!