the diameter of a sphere is
 .
.
Step-by-step explanation:
Here we have , a sphere with a volume of 4397 m^3 . We need to find the diameter of sphere . Let's find out:
We know that , Volume of sphere is given by formula as :
⇒
 .......(1)
.......(1)
According to question we have following parameters as :
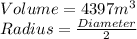
Putting these values in we get:
⇒

⇒
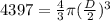
⇒
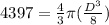
⇒
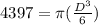
⇒
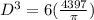
⇒

⇒
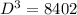
⇒
![D =\sqrt[3]{ 8402}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/r2qcfbv2mflvw0ouopvnirm9nepn1qeurk.png)
⇒

Therefore , the diameter of a sphere is
 .
.