Question

The amounts of money won by the top ten finishers in a recentDaytona 500 are listed below. Find the mean and median winnings,rounded to the nearest dollar. Which measure, the mean or themedian, best represents the data? Explain your reasoning.$2,194,246 $464,084 $164,096 $199,209 $438,834 $613,659 $142,884 $240,731 $145,809 $290,596

Answer 1

The mean winnings are $724,808 and the median winnings are $290,596. The median best represents the data because it is not affected by the extreme value of $5,000,000.

Step-by-step explanation:

The mean winnings can be found by adding up all the winnings and dividing by the number of winners. The median winnings can be found by arranging the winnings in ascending order and finding the middle value. For this data set, the mean winnings are $724,808 and the median winnings are $290,596.

In this case, the median best represents the data because it is not affected by the extreme value of $5,000,000. The mean is heavily influenced by outliers, so it may not accurately represent the typical winnings of the top ten finishers.

Answer 2

a. mean=$489,414.80

median=$265,664

b. Meidan. Not affected by outlier values.

Step-by-step explanation:

#Mean is calculated using the the formula:

`\bar x=(1)/(n)\sum{x_i}\\\\=(1)/(10)\sum(2194246+464084+164096+199209+438834+613659+142884+240731+145809+290596)\\\\=489414.80`

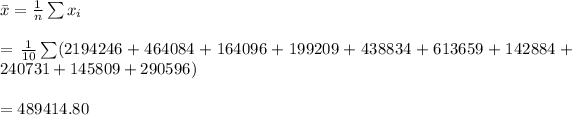
Hence, the mean winning is $489,414.80

#Our data points are even.

-We first arrange the data points in increasing order.

-The median is calculated as the average of the two middlemost data points.

Hence, the median point is $265,664

The Median is the best measure of central limit theorem as it's not affected by extreme outlier values.

-We have one outlier value of $2,194,246 which shifted the mean from $299,989.11 to $489,414.80