Question

Much appreciated if you could help. :)

Answer 1

The quadrilateral is a parallelogram because it has one pair of opposite sides that are both congruent and parallel ⇒ 2nd answer

Explanation:

The formula of a distance between two points is
`d=\sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)}`

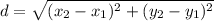
The formula of a slope of a line is
`m=(y_(2)-y_(1))/(x_(2)-x_(1))`

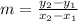
∵ L (-4 , -4) and M (-1 , -5)

∴
`x_(1)` = -4 and
`x_(2)` = -1

∴
`y_(1)` = -4 and
`y_(2)` = -5

- Use the formula of the distance to find LM

∵
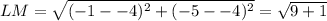
`LM=\sqrt{(-1--4)^(2)+(-5--4)^(2)}=√(9+1)`

∴ LM =
`√(10)`

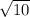
∵ J (1 , 2) and K (-2 , 3)

∴
`x_(1)` = 1 and
`x_(2)` = -2

∴
`y_(1)` = 2 and
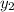`y_(2)` = 3

- Use the formula of the distance to find JK

∵
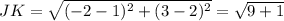
`JK=\sqrt{(-2-1)^(2)+(3-2)^(2)}=√(9+1)`

∴ JK =
`√(10)`

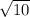
- ML and JK have equal lengths

∴ LM ≅ JK

Use the formula of the slope to find the slopes of LM and JK

∵
`m_(LM)=(-5--4)/(-1--4)=(-5+4)/(-1+4)`

∴
`m_(LM)=-(1)/(3)`

∵
`m_(JK)=(3-2)/(-2-1)=(1)/(-3)`

∴
`m_(JK)=-(1)/(3)`

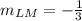
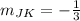
- ML and JK have same slopes

∴ LM // JK

∵ LM and JK are opposite sides in the quadrilateral

∵ LM ≅ JK

∵ ML // Jk

- Two opposite sides in the quadrilateral JKLM are congruent

and parallel

∴ JKLM is a parallelogram

The quadrilateral is a parallelogram because it has one pair of opposite sides that are both congruent and parallel