Answer:
62 MPa
Step-by-step explanation:
We are given that
Critical resolved shear stress for a metal,
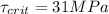
We have to find the maximum possible yield strength for a single crystal of this metal that is pulled in tension.
Yield strength,
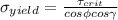
Minimum stress is necessary to introduce yielding when
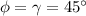
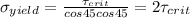
Substitute the values
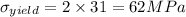
Hence, the maximum possible yield strength for a single crystal of this metal that is pulled in tension=62 MPa