Question

3. Solve the inequality and graph the solutions.
-5x < 15

Answer 1

`\boxed{{x} > -3}`

Explanation:

Given inequality:

• 
  `-5x < 15`

To solve this inequality, we need to isolate the variable on one side and the constant on the other. To do this, we can divide both sides by -5.

`\rightarrowtail -5x < 15`

`\rightarrowtail (-5x)/(-5) < (15)/(-5)`

`\rightarrowtail x < (15)/(-5)`

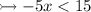
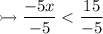
Note: If we are dividing both sides by a negative integer, the sign changes.

`\rightarrowtail {x} > (15)/(-5)`

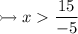
To simplify 15/-5, we can multiply -1 to the numerators and the denominators. As a result, the negative sign should transfer to the numerator, as when two negative integers multiply each other, the result is a positive integer.

`\rightarrowtail {x} > (15)/(-5) * (-1)/(-1)`

`\rightarrowtail {x} > (-15)/(5)`

`\rightarrowtail \boxed{{x} > -3}`

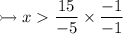
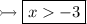
Graph:

Answer 2

`\huge\text{Hey there!}`

`\mathsf{-5x < 15}\\\\\large\text{DIVIDE -5 to BOTH SIDES}\\\\\mathsf{(-5x)/(-5) < (15)/(-5)}\\\\\large\text{SIMPLIFY IT!}\\\\\mathsf{x > -3}\\\\\huge\textbf{Therefore, your answer is: \boxed{\mathsf{x > -3}}}\huge\checkmark`

~
`\frak{Amphitrite1040:)}`