Answer:
327.5 feet²
Explanation:
Let's divide the figure into multiple shapes (Refer to image). To determine the area of the figure, we need to find the area of the divided shapes, then sum it up to obtain the area of the figure.
Determining the area of the triangle:
Given dimensions:
Determining the base of the triangle:
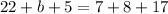
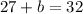
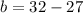
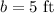
Substituting the base and the height:
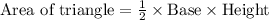
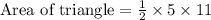
Simplifying the R.H.S to determine the area:
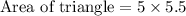
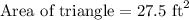
Determining the area of rectangle₁
Given dimensions:
- Length = 17 feet
- Breadth = 5 feet
Substitute the length and the breadth:
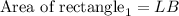
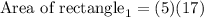
Simplify the R.H.S to determine the area:
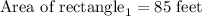
Determining the area of rectangle₂
Given dimensions:
- Length = 5 + 7 feet
- Breadth = 8 feet
Substitute the length and the breadth:
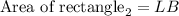
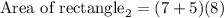
Simplify the R.H.S to determine the area
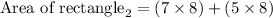
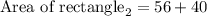
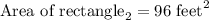
Determining the area of rectangle₃
Given dimensions:
- Length = 17 feet
- Breadth = 7 feet
Substitute the length and the breadth:
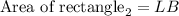
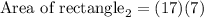
Simplify the R.H.S to determing the area:
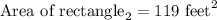
Determining the area of the figure:
A (Figure) = A (Triangle) + A (Rectangle₁) + A (Rectangle₂) + A(Rectangle₃)
= 27.5 + 85 + 96 + 119
= 327.5 feet²