Given:
The two equations are
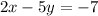 and
and
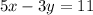
We need to solve the equations using elimination method.
Elimination method:
Let us multiply the equation
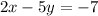 by 5, we get;
by 5, we get;
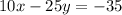 ---------(1)
---------(1)
Now, multiplying the equation
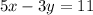 by -2, we get;
by -2, we get;
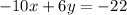 --------(2)
--------(2)
Adding equations (1) and (2), we have;

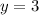
Thus, the value of y is 3.
Substituting
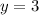 in the equation
in the equation
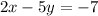 , we have;
, we have;
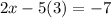
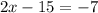
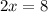
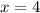
Thus, the value of x is 4.
Hence, the solution of the system of equations is (4,3)
Therefore, Option A is the correct answer.