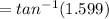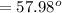Answer:
The magnitude of the force is
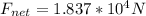
the direction is 57.98° from the horizontal plane in a counter clockwise direction
Step-by-step explanation:
From the question we are told that
At t = 0 ,
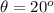
The rate at which the angle increases is
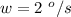
Converting this to revolution per second
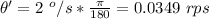
The length of the rope is defined by
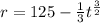
At
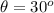 , The tension on the rope T = 18 kN
, The tension on the rope T = 18 kN
Mass of the para-sailor is
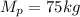
Looking at the question we see that we can also denote the equation by which the length is defied as an an equation that define the linear displacement
Now the derivative of displacement is velocity
So
![r' = -(1)/(3) [(3)/(2) ] t^{(1)/(2) }](https://img.qammunity.org/2021/formulas/physics/college/tk1i5sqjdfyitpa7v94dzn4mr3h3npithn.png)
represents the velocity, again the derivative of velocity gives us acceleration
So
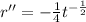
Now to the time when the rope made angle of 30° with the water
generally angular velocity is mathematically represented as
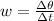
Where
 is the angular displacement
is the angular displacement
Now considering the interval between
 we have
we have
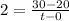
making t the subject

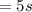
Now at this time the displacement is

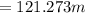
The linear velocity is
![r' = -(1)/(3) [(3)/(2) ] (5)^{(1)/(2) }](https://img.qammunity.org/2021/formulas/physics/college/s1hbpjtukvgtisvls3kvqmfz97k5bhqc27.png)
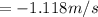
The linear acceleration is
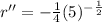
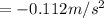
Generally radial acceleration is mathematically represented by
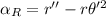
![= -0.112 - (121.273)[0.0349]^2](https://img.qammunity.org/2021/formulas/physics/college/pnc9pyimvu4js6irg4qatsbnfnjwtqcy2z.png)
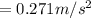
Generally angular acceleration is mathematically represented by
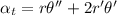
Now
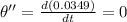
So
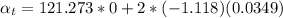
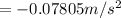
The net resultant acceleration is mathematically represented as

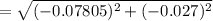

Now the direction of the is acceleration is mathematically represented as
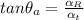
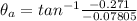
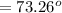
The force on the para-sailor along y-axis is mathematically represented as

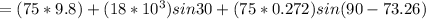
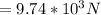
The force on the para-sailor along x-axis is mathematically represented as
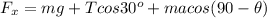
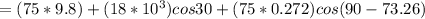
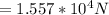
The net resultant force is mathematically evaluated as
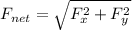
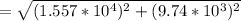
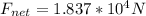
The direction of the force is
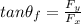
![\theta_f = tan^(-1) [(1.557*10^4)/(9.74*10^3) ]](https://img.qammunity.org/2021/formulas/physics/college/mt4el4ebm1ct6ebag4hkcoen4pfv9dmcfv.png)