Question

Calculate the ph at of a solution of sodium hypochlorite . note that hypochlorous acid is a weak acid with a of . round your answer to decimal place.

Answer 1

The question is incomplete, here is the complete question:

Calculate the pH at 25°C of a 0.39 M solution of sodium hypochlorite NaClO. Note that hypochlorous acid HClO is a weak acid with a pKa of 7.50. Round your answer to 1 decimal place.

Answer: The pH of the solution is 10.4

Step-by-step explanation:

We are given:

Molarity of sodium hypochlorite = 0.39 M

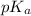`pK_a` of HClO = 7.50

We know that:

`pK_a=-\log K_a`

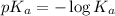
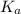`K_a` of HClO =
`10^(-7.50)=3.16* 10^(-8)`

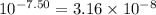
To calculate the base dissociation constant for the given acid dissociation constant, we use the equation:

`K_w=K_b* K_a`

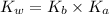
where,

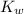`K_w` = Ionic product of water =
`10^(-14)`

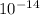
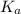`K_a` = Acid dissociation constant =
`3.16* 10^(-8)`

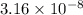
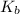`K_b` = Base dissociation constant

Putting values in above equation, we get:

`10^(-14)=3.16* 10^(-8)* K_b\\\\K_b=(10^(-14))/(3.16* 10^(-8))=3.16* 10^(-7)`

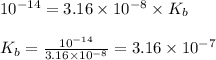
The chemical equation for the reaction of hypochlorite ion with water follows:

`ClO^-+H_2O\rightarrow HClO+OH^-`

Initial: 0.39

At eqllm: 0.39-x x x

The expression of
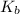`K_b` for above equation follows:

`K_b=([HClO][OH^-])/([ClO^-])`

Putting values in above equation, we get:

`3.16* 10^(-7)=(x* x)/((0.39-x))\\\\x=-0.00035,0.00035`

Neglecting the negative value of 'x' because concentration cannot be negative

To calculate the pOH of the solution, we use the equation:

`pOH=-\log[OH^-]`

We are given:

`[OH^-]=0.00035M`

Putting values in above equation, we get:

`pOH=-\log (0.00035)=3.6`

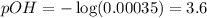
To calculate pH of the solution, we use the equation:

`pH+pOH=14\\pH=14-3.6=10.4`

Hence, the pH of the solution is 10.4