Question

Calculate the pH during the titration of 20.00 mL of 0.1000 M trimethylamine, (CH3)3N(aq), with 0.2000 M HCl(aq) after 7.5 mL of the acid have been added. Kb of trimethylamine = 6.5 x 10-5.

Answer 1

Answer: The pH of the solution is 9.33

Step-by-step explanation:

To calculate the number of moles for given molarity, we use the equation:

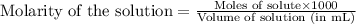`\text{Molarity of the solution}=\frac{\text{Moles of solute}* 1000}{\text{Volume of solution (in mL)}}` .....(1)

• For HCl:

Molarity of HCl solution = 0.200 M

Volume of solution = 7.5 mL

Putting values in equation 1, we get:

`0.200M=\frac{\text{Moles of HCl}* 1000}{7.5}\\\\\text{Moles of HCl}=(0.200* 7.5)/(1000)=0.0015mol`

• For trimethylamine:

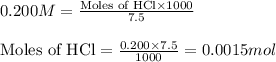
Molarity of trimethylamine solution = 0.100 M

Volume of solution = 20 mL

Putting values in equation 1, we get:

`0.100M=\frac{\text{Moles of trimethylamine}* 1000}{20}\\\\\text{Moles of trimethylamine}=(0.100* 20)/(1000)=0.002mol`

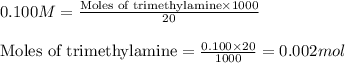
The chemical reaction for trimethylamine and HCl follows the equation:

`(CH_3)_3N+HCl\rightarrow (CH_3)_3NH^++Cl^-`

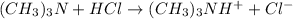
Initial: 0.002 0.0015

Final: 0.0005 - 0.0015

Total volume of the solution = [20 + 7.5] = 27.5 mL = 0.0275 L (Conversion factor: 1 L = 1000 mL)

To calculate the pH of basic buffer, we use the equation given by Henderson Hasselbalch:

`pOH=pK_b+\log(\frac{[\text{conjugate acid}]}{[\text{base}]})`

`pOH=pK_b+\log(([(CH_3)_3NH^+])/([(CH_3)_3N]))`

where,

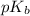`pK_b` = negative logarithm of base dissociation constant of trimethylamine = 4.19

`[(CH_3)_3NH^+]=(0.0015)/(0.0275)`

`[(CH_3)_3NH]=(0.0005)/(0.0275)`

pOH = ?

Putting values in above equation, we get:

`pOH=4.19+\log(((0.0015/0.0275))/((0.0005/0.0275)))\\\\pOH=4.67`

To calculate pH of the solution, we use the equation:

`pH+pOH=14\\pH=14-4.67=9.33`

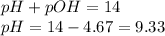
Hence, the pH of the solution is 9.33