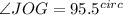Question

Cherie is jogging around a circular track. She

started at point J and has jogged 200 yards to

point G. If the radius of the track is 120 yards,

what is the measure to the nearest tenth of a

degree of minor angle JOG?

Answer 1

Measure of minor angle JOG is
`95.5^(\circ)`

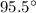
Explanation:

Consider a circular track of radius 120 yards. Assume that Cherie starts from point J and runs 200 yards up to point G.

`\therefore m JG = 200 yards, JO=120 yards`.

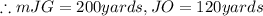Now the measure of minor arc is same as measure of central angle. Therefore minor angle is the central angle
`\angle JOG = \theta`.

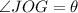To calculate the central angle, use the arc length formula as follows.

`Arc\:Length\left(s\right) = r\:\theta`

Where
`\theta` is measured in radian.

Substituting the value,

`200=120\:\theta`

Dividing both side by 120,

`(200)/(120)=\theta`

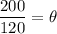
Reducing the fraction into lowest form by dividing numerator and denominator by 40.

`\therefore (5)/(3)=\theta`

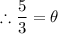
Therefore value of central angle is
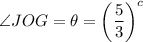`\angle JOG = \theta=\left((5)/(3)\right)^(c)`, since angle is in radian

Now convert radian into degree by using following formula,

`1^(c)=\left((180)/(\pi)\right)^(\circ)`

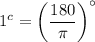
So multiplying
`\theta` with
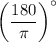`\left((180)/(\pi)\right)^(\circ)` to convert it into degree.

`\left((5)/(3)\right)^(c)=\left((5)/(3)\right) * \left((180)/(\pi)\right)^(\circ)`

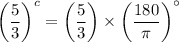
Simplifying,

`\therefore \theta = 95.49^(circ)`

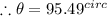
So to nearest tenth,
`\angle JOG=95.5^(circ)`