Question

3. The common musk turtle, also called a “stinkpot,” has a length of 7.60 cm at maturity. Suppose a turtle with this length is placed in front of a diverging lens that has a 14.0 cm focal length. If the turtle’s image is 4.00 cm across, how far is the turtle from the lens? How far is the turtle’s image from the lens?

Answer 1

1) 12.6 cm

2) -6.6 cm

Step-by-step explanation:

We can solve this problem by using two equations:

1) Lens equation:

`(1)/(f)=(1)/(p)+(1)/(q)`

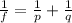
where

f is the focal length of the lens

p is the distance of the object from the lens

q is the distance of the image from the lens

2) Magnification equation:

`(y')/(y)=-(q)/(p)`

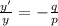
where

y' is the size of the image

y is the size of the object

In this problem we have:

y = 7.60 cm (size of the turtle)

y'= 4.00 cm (size of the image

So from eq.(2) we get

`q=-p(y')/(y)=-p(4.00)/(7.60)=-0.526p`

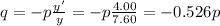
Substituting into eq(1), we can find the value of p:

`(1)/(f)=(1)/(p)-(1)/(0.526p)`

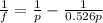
Here we have

f = -14.0 cm is the focal length (negative for a diverging lens)

So we find

`-(1)/(14.0)=(1)/(p)-(1.901)/(p)=(0.901)/(p)\\p=(-0.901\cdot 14.0)/(1)=12.6 cm`

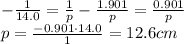
2)

Now we want to find how far is the turtle's image from the lens: so, we want to find the value of q.

We can do it by using the magnification equation:

`(y')/(y)=-(q)/(p)`

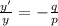
where here we have:

y' = 4.00 cm is the size of the image

y = 7.60 cm is the size of the object

p = 12.6 cm is the distance of the object from the lens

q is the distance of the image from the lens

Solving for q we find:

`q=-p(y')/(y)=-(12.6)(4.00)/(7.60)=-6.6 cm`

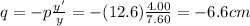
And the negative sign means the image is virtual.