Question

The sides of two similar hexagons are in the ratio 7 : 4. If the area of the smaller hexagon is 368 ft2, what is the area of the larger hexagon?

Answer 1

The area of the larger hexagon is 1126.74 ft²

Step-by-step explanation:

Given:

Ratio of sides of two hexagons = 7 : 4

Area of the smaller hexagon = 368 ft²

Area of the larger hexagon = ?

We know:

Area of hexagon =
`(3√(3) )/(2) a^2`

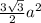
where,

a = side of the hexagon

According to the question:

`368 = (3√(3) a^2)/(2) \\\\a^2 = (368X 2)/(3√(3) ) \\\\a^2 = 141.64\\\\a = 11.9`

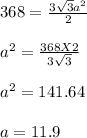
Therefore, the side of smaller hexagon is 11.9

So,

`(7)/(4) = (x)/(11.9) \\\\x = 20.825`

Therefore, the length of larger hexagon is 20.825

Area of larger hexagon =
`(3√(3)(x)^2 )/(2)`

=
`(3X√(3) (20.825)^2)/(2)`

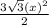
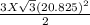
= 1126.74 ft²

Therefore, the area of the larger hexagon is 1126.74 ft²