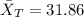Question

CitiBank recorded the number of customers to use a downtown ATM during the noon hour on 32 consecutive workdays. 27 11 36 22 36 12 35 37 50 16 31 45 48 14 20 34 46 15 25 41 34 39 42 29 32 32 8 32 20 38 43 45 Click here for the Excel Data File (a) Find the mean, midrange, geometric mean, and 14 percent trimmed mean. (Round your answers to 2 decimal places.)

Answer 1

`\bar X =  31.09`

`Midrange = (50+8)/(2)= 29.00`

`\bar G = (x_1 *x_2*...*X_(32))^{(1)/(32)} = 28.33`

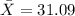
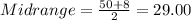
If we Trim the top and bottom 14% from the data we need to eliminate 32*0.14 =4.48 so we need to eliminate approximately 5 values from each tail and we got:

16 20 20 22 25 27 29 31 32 32 32 34 34 35 36 36 37 38 39 41 42 43

And the mean calculated from this data is :

`\bar X_(T)= 31.86`

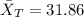
Explanation:

For this case we have the following data:

27 11 36 22 36 12 35 37 50 16 31 45 48 14 20 34 46 15 25 41 34 39 42 29 32 32 8 32 20 38 43 45

And we can calculate the mean with this formula:

`\bar X =(\sum_(i=1)^n X_i)/(n)`

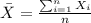
And replacing we got:

`\bar X =  31.09`

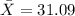
The mid range is calculated with this formula:

`Midrange = (High +Low)/(2)`

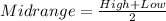
And replacing we got:

`Midrange = (50+8)/(2)= 29`

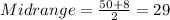
Since the sample size is n =32 we can calculate the geometric mean with this formula:

`\bar G = (x_1 *x_2*...*X_(32))^{(1)/(32)} = 28.33`

For the trimmed mean we need to sort the dats on increasing order and we got:

8 11 12 14 15 16 20 20 22 25 27 29 31 32 32 32 34 34 35 36 36 37 38 39 41 42 43 45 45 46 48 50

If we Trim the top and bottom 14% from the data we need to eliminate 32*0.14 =4.48 so we need to eliminate approximately 5 values from each tail and we got:

16 20 20 22 25 27 29 31 32 32 32 34 34 35 36 36 37 38 39 41 42 43

And the mean calculated from this data is :

`\bar X_(T)= 31.86`