Question

What is f(x) = x2 – 8x + 11 written in vertex form? f(x) = (x – 4)2 – 5 f(x) = (x – 4)2 + 5 f(x) = (x + 4)2 – 27 f(x) = (x + 4)2 + 27

Answer 1

Y= (x - 4) ^2 -5 The answer is A

Answer 2

Given:

The equation of the function is
`f(x)=x^2-8x+11`

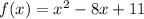
We need to determine the vertex form.

Vertex form:

The vertex form of the equation of the parabola can be determined by solving the function
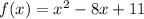`f(x)=x^2-8x+11` using completing the square method.

The vertex form of the function is of the form
`f(x)=a(x-h)^2+k`

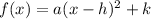
We need to write the vertex form of the function in the form of
`f(x)=a(x-h)^2+k`

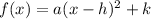
Hence, let us solve the function
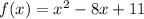`f(x)=x^2-8x+11` using completing the square method.

Thus, we have;

`f(x)=(x^2-8x+16)-5`

`f(x)=(x-4)^2-5`

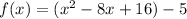
Thus, the vertex form of the function is
`f(x)=(x-4)^2-5`

Hence, Option A is the correct answer.