Answer:
72.04 dB.
Step-by-step explanation:
The intensity level of 60dB corresponds to the sound intensity
 given by the equation
given by the equation

where
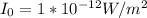
solving for
 we get:
we get:
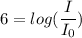
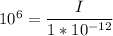

Now, when 16 violins are playing the intensity
 becomes
becomes

which on the decibel scale gives
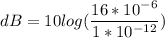
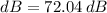 .
.
Thus, playing 16 violins together gives the intensity level of 72 dB.