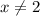Answer:
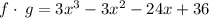
Domain: All real numbers
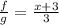
Domain: x≠2
Explanation:
The given functions are

and
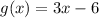
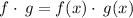
This implies that:
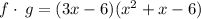
We expand to get:
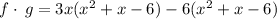
We expand to get:
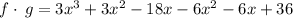
We group like terms to get:
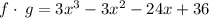
This is a polynomial function, the domain is all real.
Also;
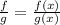
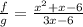
Factor to get:
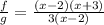
Cancel common factors:
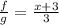
The domain is all real numbers, except numbers that will make the denominator zero.