Answer:
The rectangular form of the r=6sinθ-2cosθ is x= -1 , y= 3 and r=
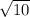 , i.e
, i.e
R(-1,3) and r=
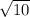 .
.
Explanation:
Given:
Equation in polar form as ; r=6sinθ-2cosθ.
To find ;
Rectangular form of given Polar form .
Solution:
We know that relationship between the polar and rectangular co-ordinates.
Hence,
r=√x²+y²
Sin∅=y/r
Cos∅=x/r
Tan∅=y/x.
Using above relations in given form,
r=6sin∅-2cos∅
r=6(y/r)-2(x/r)
x²+y²=6y-2x
x²+2x+y²-6y=0
This above equation is of the circle
Now calculating the center and radius of circle will be give us the rectangular coordinate for the given equation.
adding '1' and '9' we get completing square on both sides
x²+2x+y²-6y+1+9=1+9.
(x²+2x+1)+ (y²-6y+9)=10.
(x+1)²+(y-3)²=(√10)².
Hence comparing with standard equation of circle as ,
(x-h)²+(y-k)²=r².
here,
x-h=x+1,
h=-1,
And
y-k=y-3
k=3.
Hence coordinate are (-1,3) with radius √10.