They forget to say "not to scale". I'm guessing this is trig because I don't see another way to do it.
Let's consider x=chord PQ first. By the Law of Cosines
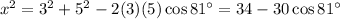
We have an isosceles triangle formed by two radii of 9 cm and x=PQ. By the Law of Cosines again,

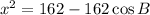
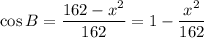
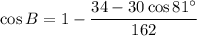

The area of the circle is the fraction given by the angle,
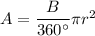
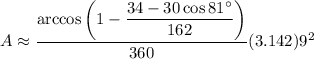
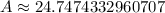
Answer: 24.7 sq cm