Question

Find the 7th term in the sequence
with the following definition:
a1 = 64
|
0

Answer 1

The answer is 1

Explanation:

Answer 2

Given:

The first term of the sequence is
`a_1=64`

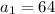
The nth term of the sequence is
`a_n=(a_(n-1))/(2)`

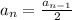
We need to determine the 7th term of the sequence.

Second term:

Substituting n = 2 in the nth term of the sequence, we get;

`a_2=(a_(2-1))/(2)`

`a_2=(a_(1))/(2)`

`a_2=(64)/(2)`

`a_2=32`

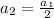
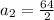
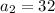
Thus, the second term of the sequence is 32.

Third term:

Substituting n = 3 in the nth term of the sequence, we get;

`a_3=(a_(3-1))/(2)`

`a_3=(32)/(2)`

`a_3=16`

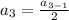
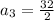
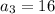
Thus, the third term of the sequence is 16.

Fourth term:

Substituting n = 4 in the nth term of the sequence, we get;

`a_4=(a_(4-1))/(2)`

`a_4=(16)/(2)`

`a_4=8`

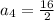
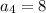
Thus, the fourth term of the sequence is 8.

Fifth term:

Substituting n = 5 in the nth term of the sequence, we get;

`a_5=(a_(5-1))/(2)`

`a_5=(8)/(2)`

`a_5=4`

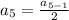
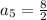
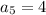
Thus, the fifth term of the sequence is 4.

Sixth term:

Substituting n = 6 in the nth term of the sequence, we get;

`a_6=(a_(6-1))/(2)`

`a_6=(4)/(2)`

`a_6=2`

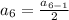
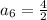
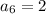
Thus, the sixth term of the sequence is 2.

Seventh term:

Substituting n = 7 in the nth term of the sequence, we get;

`a_7=(a_(7-1))/(2)`

`a_7=(2)/(2)`

`a_7=1`

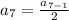
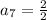
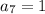
Thus, the seventh term of the sequence is 1.